< home

Machine Learning Methods in R

November 2020

Source

An almost comprehensive project comparing and analyzing basic machine learning methods, from simple linear regression to support vector machines and random forest, on a moderate-size construction raw materials dataset with 12 continuous inputs and two discrete inputs.

Requirements

Machine Learning Methods Used

Code

Exploratory Data Analysis (EDA):

# Some code snippets

# Read in data
data_url <- 'https://raw.githubusercontent.com/jyurko/CS_1675_Fall_2020/master/HW/final_project/cs_1675_final_project_data.csv'

df <- readr::read_csv(data_url, col_names = TRUE)

step_1_df <- df %>% select(xA, xB, x01:x06, response_1)

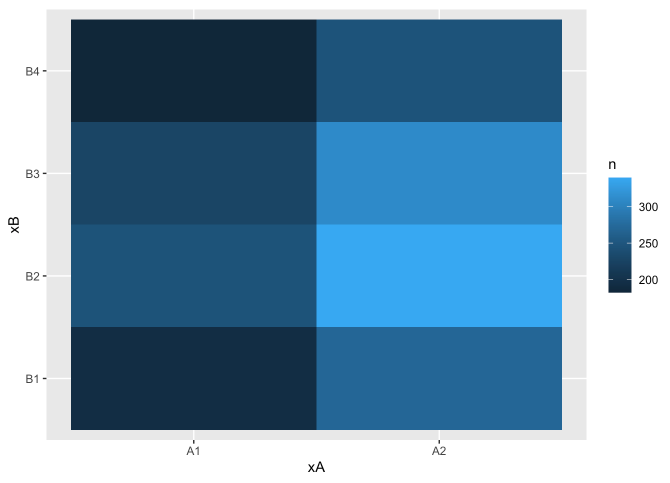
# Variation within variables
## Boxplots
step_1_df %>% tibble::rowid_to_column() %>% 
  tidyr::gather(key = "key", value = "value", -rowid, -response_1, -xA, -xB) %>% 
  mutate(input_number = as.numeric(stringr::str_extract(key, "\\d+"))) %>% 
  ggplot(mapping = aes(x = input_number, y = value)) +
  geom_boxplot(mapping = aes(group = input_number)) +
  theme_bw()

EDA boxplots

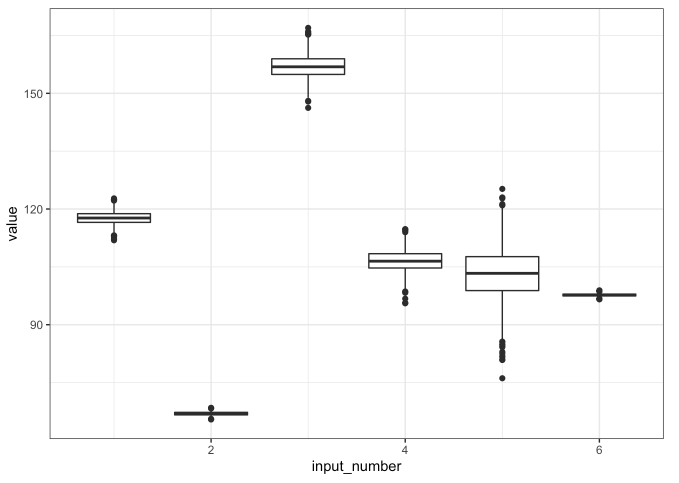
# Covariation between variables
## geom_tile (between categorical inputs)
df %>% 
  count(xA, xB) %>% 
  ggplot(mapping = aes(x = xA, y = xB)) +
  geom_tile(mapping = aes(fill = n))

EDA geom_tile

Examine part i

Regression Analysis:

# lm() to all inputs
mod_lm_step1 <- lm(response_1 ~ ., step_1_df)

# lm() to a self-devised basis function
mod_lm_basis <- lm(response_1 ~ xA + xB*(splines::ns(x01, df = 2) + splines::ns(x02, df = 2) + splines::ns(x03, df = 2)), step_1_df)

Examine part iiA Examine part iiB Examine part iiB

Binary Classification Analysis:

# Training control settings
my_ctrl <- caret::trainControl(method = "repeatedcv", 
                               number = 5, 
                               repeats = 5, 
                               savePredictions = TRUE, 
                               summaryFunction = twoClassSummary, 
                               classProbs = TRUE)
roc_metric <- "ROC"

# Logistic regression with additive terms
set.seed(12345)
mod_glm <- caret::train(outcome_2 ~ .,
                            method = "glm", 
                            metric = roc_metric, 
                            trControl = my_ctrl,
                            preProcess = c("center", "scale"),
                            data = step_2_b_df)

confusionMatrix.train(mod_glm)

# Regularized regression with elastic net
## Custom tuning grid
enet_grid <- expand.grid(alpha = seq(0.1, 0.9, by = 0.1),
                         lambda = exp(seq(-6, 0.5, length.out = 25)))

set.seed(12345)
mod_glmnet_2_b <- caret::train(outcome_2 ~ (.)^2,
                               method = "glmnet",
                               preProcess = c("center", "scale"),
                               tuneGrid = enet_grid,
                               metric = roc_metric,
                               trControl = my_ctrl,
                               data = step_2_b_df)

Examine part iii Examine part iv

Interpretation of Results:

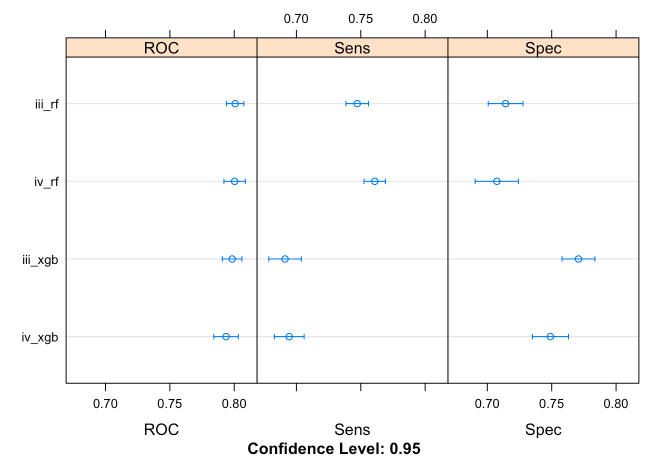
# Evaluating response_1 as a feature
## Area under the ROC curve (AUC)
results <- resamples(list(iii_rf = iii_models$iii_rf,
                          iii_xgb = iii_models$iii_xgb,
                          iv_rf = iv_models$iv_rf,
                          iv_xgb = iv_models$iv_xgb))

dotplot(results)

## Based on AUC, models including response_1 (intermediate input) as feature yield better performance in predicting outcome_2 (output variable); observed from the higher AUC values

Results response_1 AUC

# Variable importance
## Models with response_1 as a feature
plot(varImp(iii_models$iii_rf))

Results response_1 varImp

Examine part v